Research
To learn about our most recent work, please have a look at our publications.
♦ ♦ ♦
1. Innate immune responses at the single cell level: Experiments and modeling
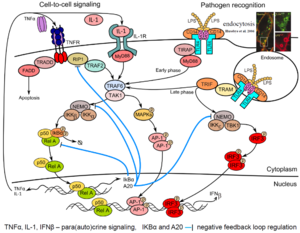
Innate immunity forms the first line of defense, limiting spread of infection before the adaptive immune response is activated. In the first phase of the innate immune response, cells detect pathogens or their fragments with their membrane and cytoplasmic receptors. This leads to activation of the regulatory systems of the transcriptional factors of NF-κB, IRF3 and AP-1 families. These factors jointly regulate the activity of several hundred genes responsible for inducing inflammation, antiviral protection, proliferation, and apoptosis. In particular, they induce production and secretion of proinflammatory cytokines (among them IL-1, TNFα) as well as interferons-α and -β. These cytokines are mediators of the second phase of the cellular innate immune response in cells that did not encounter the pathogen.
Selected publications:
- Barua D, Hlavacek WS, Lipniacki T. A computational model for early events in B cell antigen receptor signaling: analysis of the roles of Lyn and Fyn, J Immunol 189:646-658 (2012) PubMed CrossRef | PDF-ms
- Hat B, Kaźmierczak B, Lipniacki T. B cell activation triggered by the formation of the small receptor cluster: a computational study, PLoS Comput Biol 7(10):e1000448 (2011) PubMed CrossRef | PDF
- Tay S, Hughey J, Lee T, Lipniacki T, Covert M, Quake S. Single-cell NF-κB dynamics reveal digital activation and analogue information processing, Nature 466:267-271 (2010) PubMed CrossRef | PDF Code
2. Statistical methods to investigate biochemical dynamics
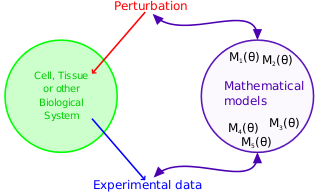
Reverse-engineering of biochemical networks is largely dependent on the quality of available data. We are interested in the development of mathematical tools to help wet experimentation in obtaining more insight about the latent mechanisms that generate experimentally observed dynamics. Specifically, we incorporate available knowledge to find experimental conditions which have a potential to reveal missing information about the studied systems. We use a variety of statistical methods ranging from bayesian statistics, through model selection, to information geometry.
Selected publications:
- Liepe J, Filippi S, Komorowski M, Stumpf MPH. Maximising the information content of experiments in systems biology, PLOS Comput Biol 9(1):e1002888 (2013) PubMed CrossRef
- Komorowski M, Costa MJ, Rand DA, Stumpf MPH. Sensitivity, robustness, and identifiability in stochastic chemical kinetics models, Proc Natl Acad Sci USA 108(21):8645-50 (2011) PubMed CrossRef
- Komorowski M, Finkenstädt B, Harper CV, Rand DA. Bayesian inference of biochemical kinetic parameters using the linear noise approximation, BMC Bioinformatics 10:343 (2009) PubMed CrossRef
3. Microfluidics for biomedical research and applications
Microfluidics have become an important tool in research and variety of industrial applications. Microfluidic devices enable precise operations on small volumes of liquids which can be obtain by the use of “smart” geometries or by the control of external devices. On the field of biological researches microfluidic devices can mimic physiological conditions better than other in vitro systems, and can be used for long term cell culture. They are controlled with high precision by external devices such pumps, valves and detectors, and can be easily automated. These features enable high throughput screening of the effects of different mixtures of reagents on the behaviour of cells, rendering microfluidics a powerful tool in research in cell biology and medicine. Microfluidics enables also the use of small droplets as separated chemical reactors or incubators. This approach which will be developed in the future enables to close the population of cells into small separated volume in which concentration of any reagent can be precisely adjusted.
Selected publications:
- Węgrzyn J, Samborski A, Reissig L, Korczyk PM, Błoński S, Garstecki P. Microfluidic architectures for efficient generation of chemistry gradations in droplets, Microfluid Nanofluid 14(1-2):235–245 (2013, e-pub 2012) CrossRef | PDF
- Jakiela S, Korczyk PM, Makulska S, Cybulski O, Garstecki P. Discontinuous transition in a laminar fluid flow: A change of flow topolgy inside a droplet moving in a micron-size channel, Phys Rev Lett 108(13):134501 (2012) PubMed CrossRef
- Korczyk PM, Cybulski O, Makulska S, Garstecki P. Effects of unsteadiness of the rates of flow on the dynamics of formation of droplets in microfluidic systems, Lab Chip 11:173-175 (2011) PubMed CrossRef
4. Modeling of calcium signaling pathways
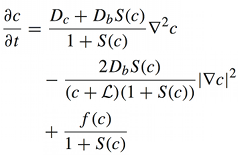
Calcium is one of the most important signaling messengers. Fundamental cellular processes are regulated by the influx of calcium from the extracellular matrix or its transport between intracellular compartments, e.g. cytosol ↔ mitochondria, mitochondria ↔ ER.
Selected publications:
- Kaźmierczak B, Peradzyński Z. Calcium waves with fast buffers and mechanical effects, J Math Biol 62:1-38 (2011, online 2010) PubMed CrossRef
- Kaźmierczak B, Volpert V. Calcium waves in systems with immobile buffers as a limit of waves for systems with non zero diffusion, Nonlinearity 21:71 (2008) CrossRef
- Kaźmierczak B, Volpert V. Travelling calcium waves in systems with non diffusing buffers, Math Mod Meth Appl Sci 18(6):883-912 (2008) CrossRef
5. Kinetic Monte Carlo simulations of biochemical reactions on the plasma membrane
Early events in cellular communication and signaling engage proteins located in the plasma membrane. Slow diffusion therein restricts the number of interacting molecules, enhancing molecular noise, and renders the membrane a spatially organized stochastic reactor. Therefore, numerical simulation of signaling on the membrane requires methods which can account for both spatial resolution and stochastic effects, such as the kinetic Monte Carlo on the lattice.
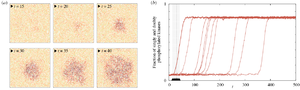
Selected publications:
- Kochańczyk M, Jaruszewicz J, Lipniacki T. Stochastic transitions in a bistable reaction system on the membrane, J R Soc Interface 10(84):20130151 (2013) PubMed CrossRef | PDF Supp-PDF Supp-movies
- Żuk PJ, Kochańczyk M, Jaruszewicz J, Bednorz W, Lipniacki T. Dynamics of a stochastic spatially extended system predicted by comparing deterministic and stochastic attractors of the corresponding birth-death process, Phys Biol 5(9):055002 (2012) PubMed CrossRef | PDF-ms
- Szymańska P, Kochańczyk M, Miększ J, Lipniacki T. Effective reaction rates in diffusion-limited phosphorylation–dephosphorylation cycles, Phys Rev E 91:022702 (2015) CrossRef | PDF-ms

